自动控制元件笔记
第一章 磁路及其计算
1.自动控制元件
- 敏感元件(测量元件)
- 放大元件
- 执行元件
- 校正元件(提高系统精度和动态性能)
2.磁路物理量和磁路基本定律
$\Phi$ 磁通,单位$Wb$;$B$ 磁感应强度,单位(T);H磁场强度,单位A/m;$\mu$磁导率,单位H/m
\[\Phi = \int_A B \cdot dA \\ H=\frac{B}{\mu}\]由介质中的Maxwell方程组中的磁场强度 \(\int_L H \cdot dL = \underset{i}{\Large \Sigma} I_i+\int_A\frac{\partial D}{\partial t}dA \xlongequal{稳恒电场}\underset{i}{\Large \Sigma} I_i\)
磁路基尔霍夫定律
- 磁路基尔霍夫第一定律(由磁场高斯定理推导得;类比节点电流净流入量为0)
- 磁路基尔霍夫第二定律(安培环路定理推到得)
磁阻推导(一般用于空气隙,因为空气为$\mu_0$,而铁磁介质中是变$\mu$) \(R_{\delta} = \frac{HL}{\Phi}=\frac{HL}{\mu H A} = \frac{L}{\mu A}\)
综合磁路基尔霍夫定律和磁阻的定义,可以画出等效磁路,并计算其中的物理量。如下图所示。
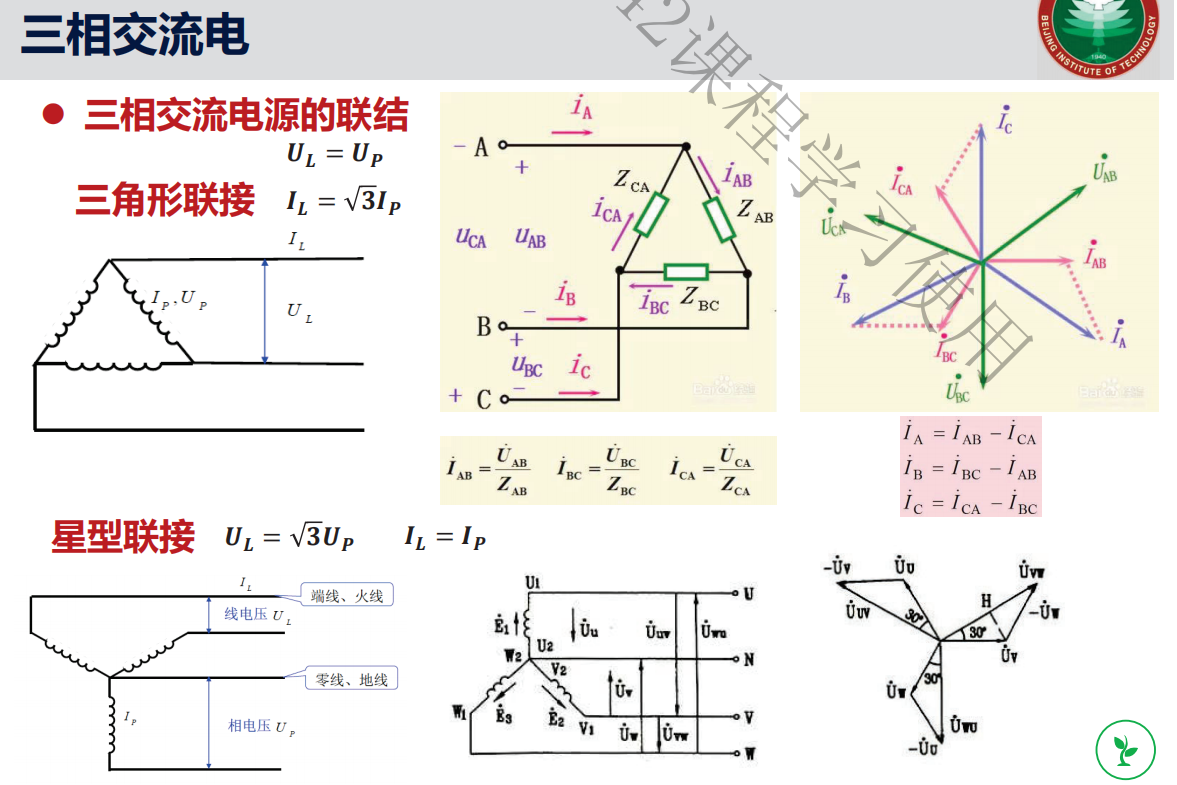
3.三相交流电
三相交流电的线圈等效为一个电阻串联上一个理想电压源,一般是三个线圈是三角形联结和星型联结。
好文欣赏第六讲 三相交流电路分析 (zhihu.com),主要讲解了相关计算
4.铁磁材料的导磁性能
- 直线为真空磁化曲线
- $a \rightarrow d $为铁磁材料的磁化曲线
剩下的是磁导率曲线
磁滞现象与磁滞回线
各磁滞回线顶点的连线为磁化曲线
- $B_r$ 为铁磁材料的剩余感应强度
- $H_c$铁磁材料的矫顽力
磁滞损耗$P_h$与材料分类
经验公式$P_h=k_h \times f \times B^{\alpha}_{m} \times V$
$k_h$磁滞损耗系数,取决于铁磁材料性质;
$f$磁场交变频率;
$B_m$磁感应强度赋值;
$V$铁心体积;
$\alpha$指数,当$B_m = 1 \sim 1.6Wb/m^2,\alpha=2$
软磁材料磁滞回线较窄,磁滞损耗较小,适合做铁心
硬磁材料磁滞回线较宽,磁滞损耗较大,适合做永久磁铁
涡流损耗
在交变磁化过程中会产生感应电势和感应电流,该电流在铁心中环绕磁力线做漩涡状分布
经验公式$P_e \propto f^2 B^{2}_{m} d^2 / \rho$
$f$磁场交变频率;
$B_m$磁感应强度赋值;
$d$铁磁材料的厚度;
$\rho$铁磁材料的电阻率
铁心损耗
- 铁心损耗包括磁滞损耗和涡流损耗
- 经验公式:$P_c = P_h + P_e = (k_hfB^{\alpha}_m+k_ef^2B^2_m)V$,其他符号与上面的定义一样。$k_e$取决于材料、叠片厚度和铁心尺寸的系数
温度特性
当铁磁材料的温度升到一定程度时,由于磁畴的方向会由于熵增而变得无须,内部铁磁材料会变为弱磁介质。电磁元件实用需要注意散热
5.磁路计算
5.1 直流磁路计算
第一类问题:已知磁通求磁势
$\Phi \rightarrow B \rightarrow 查表得磁铁中的H ;各气隙磁阻 \rightarrow 磁路定理得F、I $
第二类问题:已知磁势求磁通
猜试法
先忽略铁芯磁阻,只考虑气隙,近似得一个$\Phi_0$,按第一类问题求解得F,若偏差小于10%,则取这个值,若大于,减小$\Phi_0$重新计算,依此类推
图解法
与高中的求含有变阻值电阻的元器件的电路的求法类似,空气隙的磁阻确定。在$\Phi \sim U_m$图中画直线找交点
5.2 交流磁路计算
习题
第二章 变压器
0.三相交流电
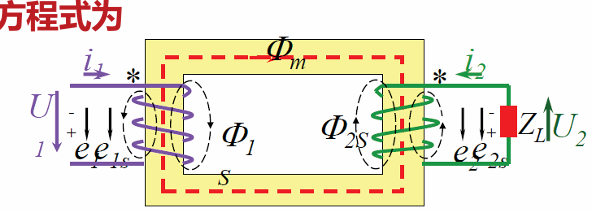
1.空载运行时的电压平衡方程
- 方程式
- 其中$e_{1s}= -\frac{d \large\Psi_{1s}}{dt}$表示漏磁在线圈1中产生的电压
- $e_{1}= -N_1\frac{d \large\Phi}{dt},e_{2}= -N_2\frac{d \large\Phi}{dt}$为两边共同的磁通产生的电压
- 向量表示
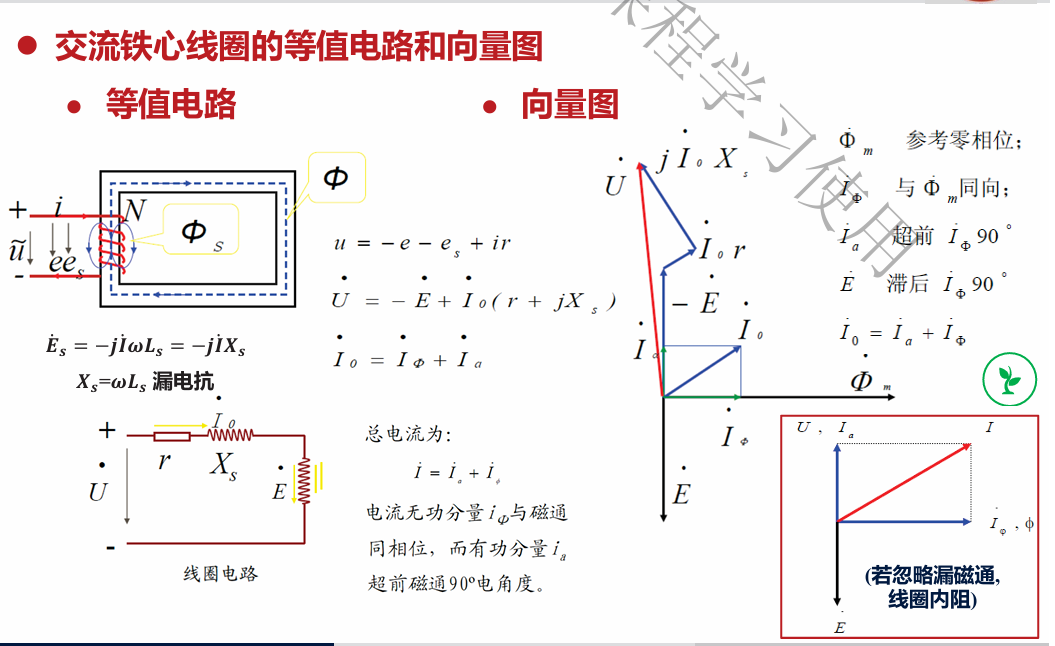
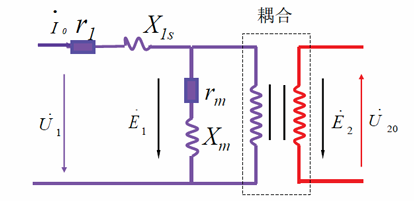
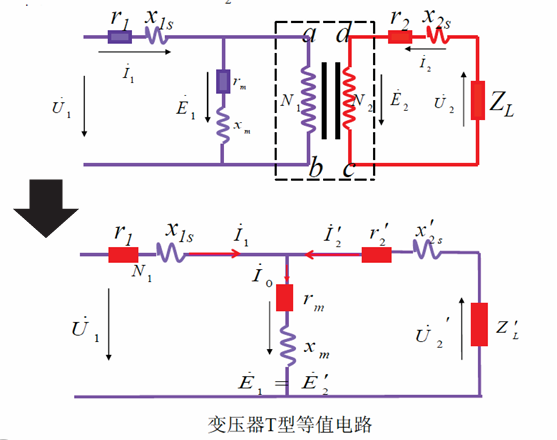
变压器的等值电路图
等值电路图中的$X_m、r_m$为激磁电抗和激磁电阻,分别表示由主磁通引起的电抗和铁心中存在的有功损耗等效电阻。能这么等效的一大原因是铁心存在饱和,$\Phi_m$变化基本呈线性,故可以等效为线性的电感
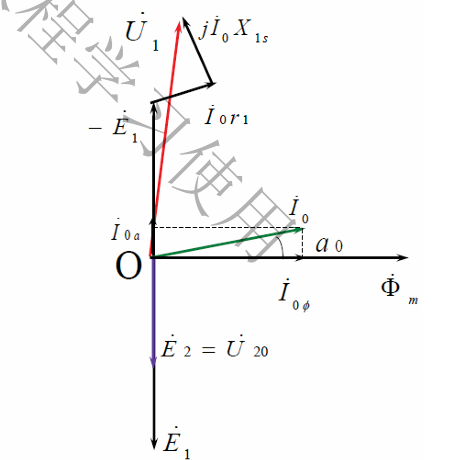
- 向量图 电流分为有功分量和励磁分量
2.单相变压器的负载运行
负载时变压器电压平衡方程式和有效向量表示,其中二次绕组的漏磁等效原理相同 \(\begin{equation} \begin{cases} u_1=-e_1-e_{1s}+i_0r_1 \\ u_{2} =e_2+e_{2s}-i_2r_2 \end{cases} \end{equation}\)
\[\begin{equation} \begin{cases} \dot U_1=-\dot E_1+\dot I_0(r_1+jX_{1s}) \\ \dot U_{2} = \dot E_2 -\dot I_2 (r_2 + jX_{2s}) \end{cases}\end{equation}\]由公式(10)中第一行,由于一次绕组的阻抗压降很小,$\dot U_1 \approx -\dot E_1 = 2 \pi f N_1 \Phi$,可见只要输入电压不变,负载的主磁通与空载时基本相同。故加上负载后需要多加一个磁势平衡方程: \(\begin{equation} \begin{cases} \dot I_1N_1 +\dot I_2N_2 =\dot I_0 N1 \\ \dot I_1 = \dot I_0 - \dot I_2 \frac{\large N_2}{\large N_1} = \dot I_0 -I^{’}_2 \end{cases} \end{equation}\) 可以发现这里电流和可以在形式上等效为并联,折合前后满足电压相等、同时功率不变,故可以折合阻抗 \(\dot I^{'}_2 = \frac{I_2}{K} , E^{'}_2 = E_2 \frac{N_1}{N_2} = E_2 K \\ Z^{'}_L+jX^{'}_{2s}+r^{'}_2 = \frac{E^{'}_{2}}{I^{'}_{2}}=K^2 \frac{E_{2}}{I_{2}}=K^2 (Z^{'}_L+jX^{'}_{2s}+r^{'}_2) \\ 由于同比例,各个阻抗可以都分别同样折合K^2\)
\(\begin{align*}\begin{cases} \dot U_1=-\dot E_1+\dot I_0(r_1+jX_{1s}) \\ \dot U_{2} = \dot E_2 -\dot I_2 (r_2 + jX_{2s}) \\ \dot E_1 = -j2\pi f N_1 \dot \Phi_m \\\dot E_2 = j2\pi f N_2 \dot \Phi_m \\\dot I_1 = \dot I_0 +(-\frac{ \large \dot I_2}{\large K})\end{cases} & \Large \Rightarrow & \begin{cases} \dot U_1=-\dot E_1+\dot I_0(r_1+jX_{1s}) \\ \dot E_1 = \dot I^{'}_2[(r^{'}_2+jX^{'}_{2s})+Z^{'}_L] \\\dot I_1 +\dot I^{'}_2 = \dot I_0 \\\dot E_1 = -\dot I_0 (r_m+ jX_m)\end{cases}\end{align*}\) 向量图如下所示:
习题
第三章 直流电机
1.直流电机的结构
禁止部分:定子(磁极,机座)
旋转部分:转子(电枢铁心,电枢绕组,换向器)
2.直流电机的电枢绕组和磁场
2.1电枢绕组
- 环形绕组 (内部磁场强度几乎为0,故内部部分的线圈没有产生力矩,造成浪费)
- 鼓形绕组
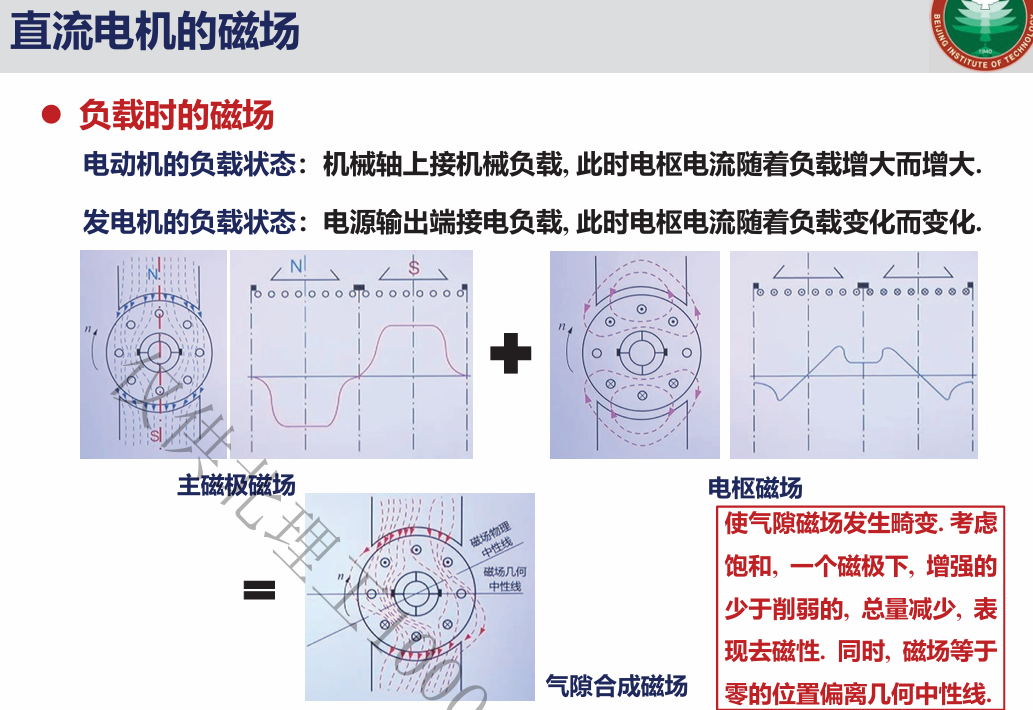
2.2 直流电机的磁场
3.直流电机的电枢电势和电磁转矩
电枢电势计算
$D$是电枢外经,$p$是磁极对数,$\tau= \frac{\pi D}{2 p}$表示正对某一个磁极的长度
$l$为元件导体有效长度
设$B_{cp}$为一个极下气隙平均磁感应强度(T),则每极磁通量$\Phi = B_{cp} \tau l$
电机转速$n$(r/min),电机转速$v= \frac{\pi D}{60}$ 每根有效导体中平均感应电势$e_{cp} = B_{cp} l v$
设绕组元件数为$S$,每一个元件$N_y$匝线圈,有效导体数$N = 2SN_y$,设绕组在两端电刷并联对数为$a$则每支电路电刷两端总的感应电势平均值: \(E_a = \frac{N}{2a} e_{cp}= \frac{N}{2a}\frac{\Phi}{\tau} v = \frac{N}{2a}\frac{\Phi}{\tau} \frac{\pi D}{60} n = \frac{pN}{60a}\Phi n = C_e \Phi n\)
计算结果表明感应电势的大小和每极的磁通和电枢转速的乘积成正比
电磁转矩计算 \(M_{em} = N f_{cp} \frac{D}{2} = N (B_{cp} \frac{I_a}{2a} l)\frac{D}{2} = N (\frac{\Phi}{\tau}\frac{I_a}{2a} )\frac{D}{2} = \frac{pN}{2 \pi a} \Phi I_a =C_m \Phi I_a\)
4.直流测速发电机
4.1分析方程
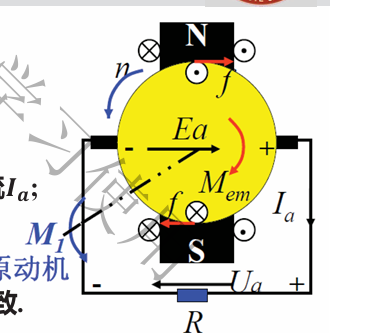
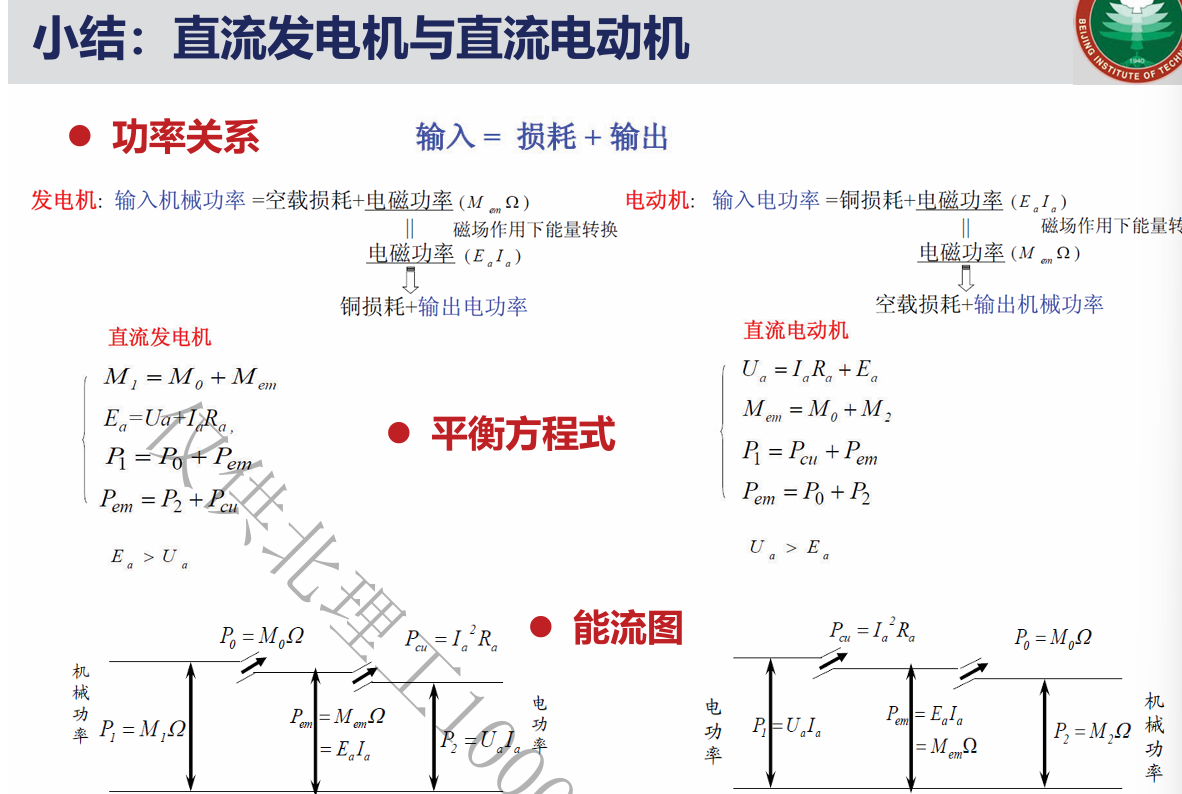
直流发电机如下图所示,设原动机提供的机械转矩为$M_1$,电枢每分钟转$n$圈,空载摩擦等产生的阻力矩为$M_0$,电枢绕组内产生感应电动势$E_a$,在外电路产生电枢电流$I_a$,电枢电流产生电磁转矩$M_{em}$
- 电势平衡方程
- 转矩平衡方程式
- 功率平衡方程式
- 整个体系的能量转换为将机械能转换为动能,即原动机转动产生的动能通过磁场转化为电能,故由上面的电势平衡方程和转矩平衡方程
- 效率
4.2直流测速发电机的特性
- 直流测速发电机的外特性
电机转速为额定$n_N$,他励直流发电机的励磁电流达到额定值$I_{jN}$时,发电机负载两端电压$U_a$与负载电流$I_a$之间的关系$U_a = f(I_a) = E_a - R_a I_a$,这里后面不成线性的原因是随着电流增大去磁作用变大,$\Phi \downarrow$,使得$ E_a \downarrow$
电压调整率定义为 如下,其中$U_{a0}$为空载时输出电压,$U_{aN}$为额定运行时输出电压 \(\Delta U_a = \frac{U_{a0}-U_{aN}}{U_{a0}}\)
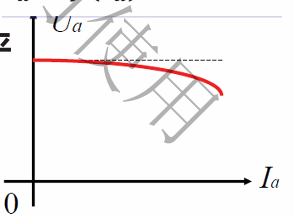
直流测速发电机的输出(静态)特性
指当励磁保持不变,负载也保持一定的情况下,发电机的转速与负载端电压之间的关系。
- 空载时:$U_a = E_a -I_a R_a$
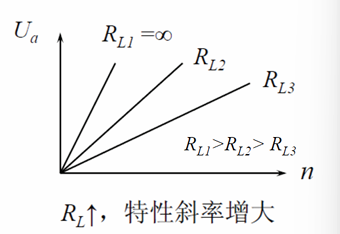
- 负载后:$U_a = \frac{E_a}{1+ \Large \frac{R_a}{R_L}} = \frac{C_e \Phi }{1+ \Large \frac{R_a}{R_L}} n$
- 如下图所示,这里忽略了$\Phi$的变化
- 控制系统对直流测速发电机的要求
- 输出特性斜率要大,电压对转速的灵敏度高
- 输出电压和转速关系为线性,输出电压正确反映电机转速
- 温度变化对特性的影响要小,内阻受温度影响,影响电流
- 输出电压纹波要小
- 正反转时,输出特性要一致
- 直流测速发电机的误差及其减小办法
- 温度的影响(一般电阻在温度$\uparrow$时$R \uparrow$,电枢阻值$R_a$和励磁电阻$R_j$(励磁电流变小)都变大,使得$U_a$减小;措施为附加负温度系数热敏电阻、磁路设计饱和)
- 电枢反应的影响。限制最小$R_L$、最大$n_{max}$
- 延迟换向的影响。换向元件上的感应电势和电流产生磁通,阻止主磁场的变化,起去磁作用,使输出特性偏离线性(限制转速)
- 电刷接触压降的影响(电刷选用接触压降小的材料)
5.直流伺服电动机
5.1直流伺服电动机分析方程
- 电势平衡方程
- 转矩平衡方程式
- 功率平衡方程式
- 整个体系的能量转换为将机械能转换为动能,即原动机转动产生的动能通过磁场转化为电能,故由上面的电势平衡方程和转矩平衡方程
5.2直流发电机与直流电动机对比小结
5.3直流伺服电动机的运行特性
## 习题
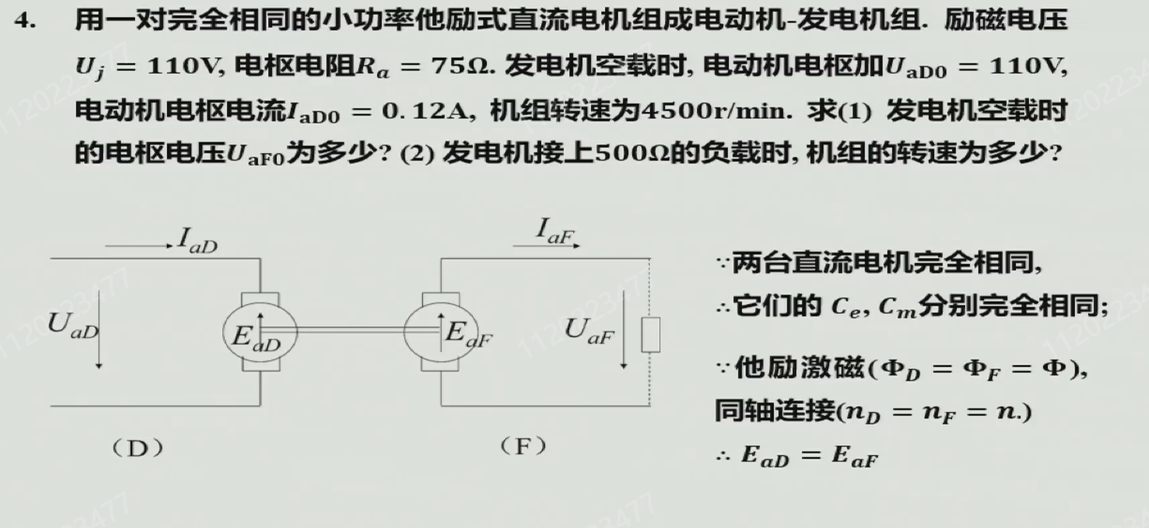
围绕以下两个公式展开 \(E_a = C_e \Phi n \\ M_{em} = C_m \Phi I_a \\ 其中,C_m = \frac{60}{2 \pi} C_e\)
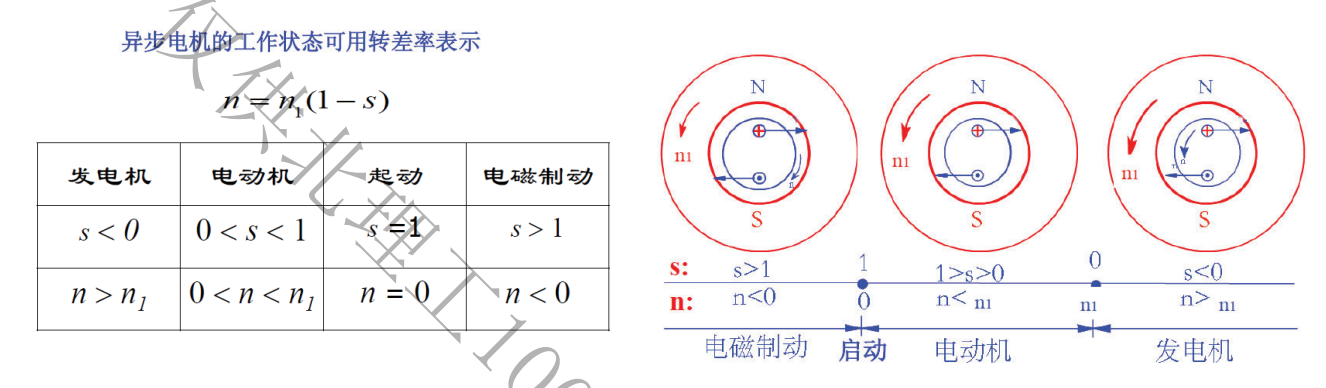
第四章 交流异步电机
1.交流异步电动机的结构和磁场
结构
每相绕组由多个线圈绕制而成,每个线圈包含$N_y$匝导体,每匝线圈有两个有效边,有效边相差180°电位角
m相绕组,极对数P,则电动机的电角度、机械角 \(电角度 = \frac{360^。}{m} \\机械角 = \frac{电角度}{P}\)
磁场
- 由磁路定理,忽略未饱和磁铁中的磁压降后,气隙中的磁势应为方波分布,为方便计算,考虑到基波幅值最大,忽略高次谐波,当成正弦计算。沿气隙在空间呈正弦分布,幅值位置不变(即磁场始终以绕组轴线对称分布),磁场大小和方向随时间作正弦变化的磁场叫交流脉振磁场,单相绕组产生的磁场就是单相脉振磁场,产生脉振磁场,产生脉振磁场的磁势称脉振磁势。
单相脉振磁势表达式(其中$ \tau = \frac{\pi D}{2 p}$,表示沿定子内表面之间的距离,$D$为定子内直径) \(f_{A}(x,t)=\frac{4}{\pi}\frac{iN_y}{2}cos\frac{\pi}{\tau}x=\frac{4}{\pi}\frac{\sqrt{2}}{2}sin\omega tIN_ycos\frac{\pi}{\tau}x\)
定子绕组合成一个旋转圆形磁场 \(n_1=\frac{60f_1}{p}(r/min)\)
交流电机的合成磁场
- 电角度和机械角度满足公式(24)的关系时,合成的磁场为圆形磁场 \(f(t) = \frac{m}{2} \frac{4}{\pi} \frac{\sqrt{2}}{2}IN_ysin\omega t \\ = \frac{m}{2} \times 0.9IN_ysin\omega t\)
2.三相交流异步电动机的运行分析
工作原理
定、转子三相对称等效(折合,$N_{1、2}$为实际每相总匝数,$k$为绕组分布系数)
- 定子 $r_1 ,L_1,N_A = …=N_1k_{N1}$
- 转子$r_2 ,L_2,N_a = …=N_2k_{N2}$
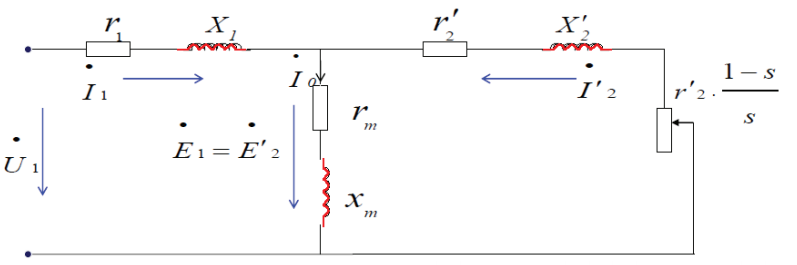
一相绕组的等值电路
类比变压器等效思路,将$X_2,r_2$进行等效,由于还对外输出机械功率,等效为电阻
等效推导过程
变比$K = \frac{N_1K_{N1}}{N_2K_{N2}}$ \(I_{2s}(f_2) = \frac{E_{2s}(f_2)}{\sqrt{r_2^2+X^2_{2s}}} = \frac{sE_2(f_1)}{\sqrt{(\frac{r_2}{s})^2+X_2^2}}=I_2(f_1) \\ r_2{'}= K^2 r_2 \\ x_2^{'}=K^2 x_2\)
电路图